Robotics represents today's highly integrated, representative high-tech field, which combines multiple disciplines. Including mechanical engineering, computer technology, control engineering, electronics, biology and other multidisciplinary intersections and integrations, reflecting the advanced level of today's practical science and technology.
In general, the robot consists of several parts, which are mechanical parts (generally referred to as mechanical arms connected by joints), sensing parts (including measuring devices for measuring position, speed, etc.), and control parts (for transmission The measurement signal from the sensing part is processed and given the corresponding control function).
As the "brain" of robots, the importance of robot control technology is self-evident.
It mainly uses the information transmitted by the sensing and other parts, and adopts the control algorithm to make the mechanical part complete the target operation and bear the corresponding part of the corresponding control function. The ultimate goal is to minimize the deviation of the actual motion trajectory of the robot from the desired target to achieve the desired motion accuracy.
The robot controller is a computer control system based on the theory of robot control technology, coupled with the kinematics and dynamics modeling of the robot. At this time, we transform a complex and abstract physical model into a relatively clear and concrete mathematical model. Once established, we will separate the control problem from the specific robot device to a certain extent. Make further understanding.
With the evolution of robot-related science and technology, control algorithms have gradually become richer, resulting in many new control strategies such as adaptive control, self-tuning control, robust control, variable structure control, nonlinear system control, and predictive control.
However, among the many excellent control algorithms, the most active ones are PID (proportional, integral, differential) control, and many advanced control strategies are also developed based on PID control algorithms.
In the development process of system control in production process, PID control is one of the oldest and most powerful basic control methods in history. It was the only control method before the 1940s, except that switch control could be used in the simplest case.
In the 20th century, communication technology and electronic technology began to develop. At the same time, war and industry have also become the driving force, and the theory of automatic control technology and automatic control has begun to develop rapidly. The birth of PID stems from human research on feedback systems.
In the 1920s, scientists at the Bell Telephone Laboratory in the United States gradually established a frequency characteristic analysis method for the feedback control system. Engineers with a communications background in Bell Labs are often familiar with the frequency domain approach.
In 1932, H. Nyquist published a paper using a graphical method to judge the stability of the system. This method was later used for the analysis and design of automatic control systems. After that, the feedback control principle began to be applied to industrial processes.
In 1934, the MIT MIT professor founded the servo control theory and first proposed the importance of trajectory tracking in feedback control. Two years later, British A. Callender and A. Stevenson gave the PID controller method.
Simply put, the advantages of PID control are three:
Mature technology and excellent control effect;
Adaptable, the PID algorithm almost meets the requirements for various process control objects;
Robust.
Among them, Robustness refers to the ability of the feedback control system to withstand the effects of such uncertainties. In simple terms, when the robustness is better, the PID algorithm can still control the attitude of the robot within a reasonable range when certain physical characteristics of the robot change.
On the one hand, PID is low-cost and easy to operate; on the other hand, most control objects can directly use PID control without having to go deep into the model mechanism, because its strong robustness can ensure that the system's performance indicators meet the basic requirements.
In general, the PID controller is a linear controller. The meaning of the PID control is that the error signals obtained after the feedback are respectively subjected to the ratio P, the integral I and the differential D operation, and then superimposed to obtain the controller output signal. In the actual working process, the system gives a given value (also called the expected value), and the actual output value measured by the measuring link is fed back to the system and will deviate from the expected value e. The role of the PID controller is to correct the deviation e.
In the specific application, we can analyze the specific problems and select different combinations of P, PI, PD and PID according to actual needs. In the actual operation process, the key of the robot control system debugging process is to adjust the coefficients of the three links of proportional, integral and differential.
With an algorithm, how do you combine it with a robot?
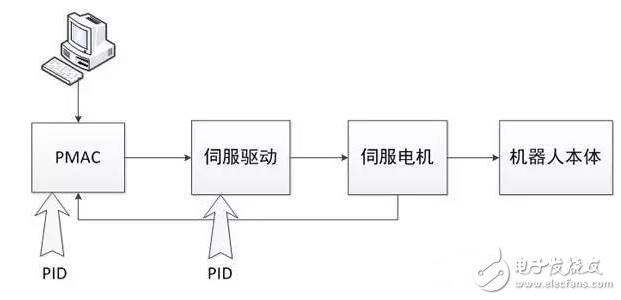
Let us give an example to illustrate. Taking wheeled robots as an example, in order to make the robot can walk agilely and stably, we need to control the servo motor that drives the robot body. First, we need to adjust the PID of the servo driver itself. Then, in order to control the effect more accurately, the system also uses an open multi-axis motion controller (PMAC), and the control card can also perform PID adjustment. The control system of the robot can be simplified into the following process.
So, what role does the ratio, integral, and differential play in the robot system?
Each of the three links has its own characteristics. Let me look at it separately:
Proportion P: It can reflect the deviation between the “current†travel speed of the robot and the set value of the control personnel. The larger the KP, the faster the system adjusts, but when it is too large, the robot motion is unstable;
Integral I: It can reflect the "cumulative" deviation of the robot. As long as there is an error, the integral link will be adjusted, and finally the adjustment will make the system unbiased, that is, the robot will reach the motion state given by the operator;
Differential D: It can predict the trend of robot movement deviation "in advance", and eliminate the error ahead of time before it is formed;
In the three links, the integral I link and the differential D link cannot be used separately, and must be used together with the proportional P link.
In this system, the controller interacts with the robot through the computer and gives corresponding control commands (such as stop, advance, etc.). The servo-driven PID controls the servo motor initially, and the servo motor's measurement signal is fed back to the open type. The multi-axis motion controller, then the PID of the controller will fine-tune the system again, so that the servo motor runs more smoothly, thus completing various operational commands of the control personnel to the wheeled robot.
Since the computer entered the field of control, a digital computer has been used instead of an analog computer controller to form a control system. In order to facilitate computer calculations, the PID can also be expressed in increments. For mechanical parts, this is very beneficial. The computer only outputs the control increments at a time. This reduces the impact of the robot failure and enables bumpless switching, while the PID control becomes more flexible. It is.
switch and socket, Wall switch and socket, push switch and socket
Guangdong Shunde Langzhi Trading CO., Ltd , https://www.langzhielectrical.com