A filter is a frequency selective device that allows specific frequency components in a signal to pass through, greatly attenuating other frequency components. With this frequency selection of the filter, interference noise can be filtered out or spectrum analysis can be performed. In other words, any device or system that can pass a particular frequency component of a signal and greatly attenuate or suppress other frequency components is referred to as a filter.

Filtering concept
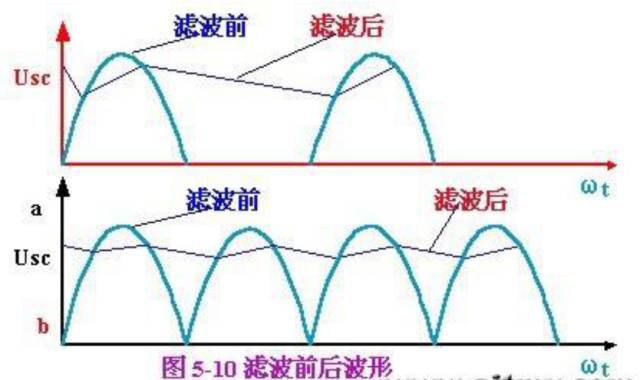
Filtering is an important concept in signal processing. The function of the filter circuit is to reduce the AC component in the pulsating DC voltage as much as possible, retain its DC component, reduce the output voltage ripple coefficient, and the waveform becomes smoother.
In general, filtering is divided into classical filtering and modern filtering.
Classical filtering is an engineering concept based on Fourier analysis and transformation. According to advanced mathematical theory, any signal that satisfies certain conditions can be regarded as being superimposed by an infinite number of sine waves.
In other words, the engineering signal is a linear superposition of sine waves of different frequencies. The sine waves of different frequencies that make up the signal are called the frequency components or harmonic components of the signal. A circuit that allows only signal components in a certain frequency range to pass normally, while blocking another part of the frequency component, is called a classical filter or a filter circuit.

In classical filtering and modern filtering, the filter model is actually the same (the hardware aspect of the filter is not much progress), but modern filtering also adds many concepts of digital filtering.
Principle of the filter circuit
When the current flowing through the inductor changes, the induced electromotive force generated in the inductor will prevent the current from changing. When the current through the inductor increases, the self-induced electromotive force generated by the inductor coil is opposite to the current direction, preventing the increase of the current, and converting a part of the electric energy into a magnetic field can be stored in the inductor; when the current through the inductor is reduced, The self-induced electromotive force is in the same direction as the current, preventing the current from decreasing and simultaneously releasing the stored energy to compensate for the decrease in current.
Therefore, after the inductance filtering, not only the ripple of the load current and the voltage is reduced, the waveform becomes smooth, and the conduction angle of the rectifier diode increases.
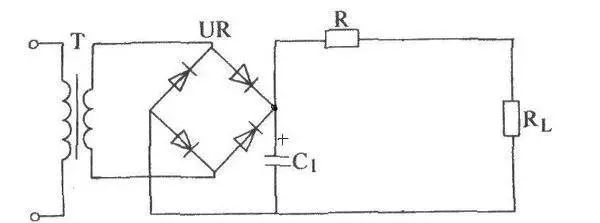
With the inductor coil unchanged, the smaller the load resistance, the smaller the AC component of the output voltage. A better filtering effect can only be obtained when RL>>ωL. The larger the L, the better the filtering effect.
The role of the filter
1. Separate the useful signal from the noise to improve the signal's anti-interference and signal-to-noise ratio;
2. Filter out frequency components that are not of interest and improve the analysis accuracy;
3. Separate a single frequency component from complex frequency components.
Ideal filter and actual filter
Ideal filter
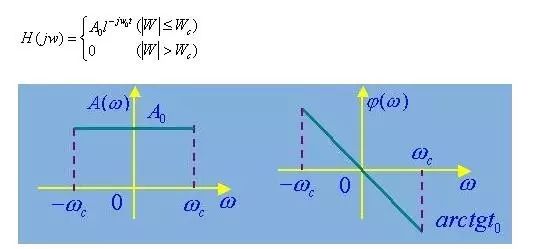
The filter does not distort the amplitude and phase of the signal in the passband, and the filter whose frequency components in the block are attenuated to zero has a clear boundary between the passband and the stopband.
For example, the frequency response function of an ideal low-pass filter is:
Actual filter
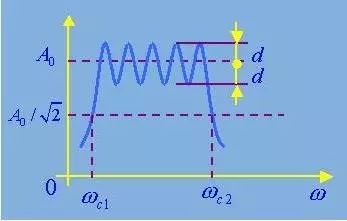
The ideal filter does not exist. In the amplitude-frequency characteristic diagram of the actual filter, there should be no strict limits between the passband and the stopband. There is a transition zone between the passband and the stopband. The frequency components in the transition zone are not completely suppressed and will only be attenuated to varying degrees.
Of course, it is desirable that the transition band is as narrow as possible, that is, it is desirable to attenuate the frequency components outside the passband as much as possible. Therefore, when designing an actual filter, it is always possible to approach the ideal filter as much as possible by various methods.
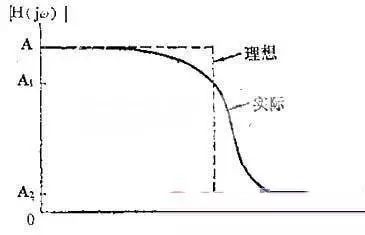
As can be seen from the amplitude-frequency characteristics of the ideal bandpass and the actual bandpass filter, the characteristics of the ideal filter need only be described by the cutoff frequency, while the characteristic curve of the actual filter has no obvious turning point, and the amplitude-frequency characteristic between the two cutoff frequencies. It is also very numerous, so it needs to be described with more parameters.
1, ripple amplitude d
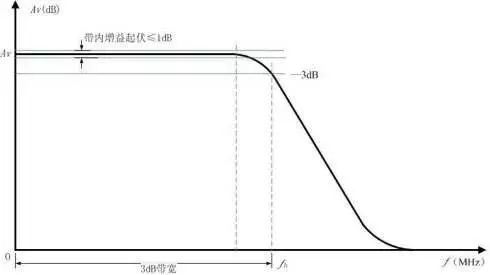
In a certain frequency range, the amplitude-frequency characteristic of the actual filter may be rippled, and the fluctuation amplitude d is smaller than the average value A0 of the amplitude-frequency characteristic, and generally should be much smaller than -3 dB.
2, cutoff frequency fc
The frequency corresponding to the amplitude-frequency characteristic value equal to 0.707A0 is called the cut-off frequency of the filter. With A0 as the reference value, 0.707A0 corresponds to the -3dB point, that is, 3dB attenuation with respect to A0. If the signal power is expressed as the square of the amplitude of the signal, the corresponding point is exactly the half power point.
3, bandwidth B and quality factor Q value
The frequency range between the upper and lower cutoff frequencies is called the filter bandwidth, or -3dB bandwidth, in Hz. The bandwidth determines the ability of the filter to separate adjacent frequency components in the signal—frequency resolution. In electrical engineering, Q is usually used to represent the quality factor of the resonant tank.
In the second-order oscillation, the Q value corresponds to the amplitude gain coefficient of the resonance point, and Q = 1/2 ξ (ξ - damping rate). For a bandpass filter, the ratio of the center frequency f0( ) to the bandwidth B is usually referred to as the quality factor Q of the filter. For example, a filter with a center frequency of 500 Hz, if the -3 dB bandwidth is 10 Hz, the Q value is said to be 50. The larger the Q value, the higher the filter frequency resolution.
4, octave selectivity W
Outside the two cutoff frequencies, the actual filter has a transition band. The slope of the amplitude-frequency curve of this transition band indicates how fast the amplitude-frequency characteristic is attenuated, which determines the filter's ability to reject the frequency components outside the bandwidth.
It is usually characterized by octave selectivity. The so-called octave selectivity refers to the attenuation value of the amplitude-frequency characteristic between the upper cutoff frequencies fc2 and 2fc2, or between the lower cutoff frequencies fc1 and fc1/2, that is, the attenuation amount or times when the frequency changes by one octave. The amount of frequency attenuation is expressed in dB/oct (octave, octave).
Obviously, the faster the attenuation (ie, the larger the W value), the better the selectivity of the filter. The attenuation rate away from the cutoff frequency can also be expressed as a 10 octave attenuation number. That is [dB/10oct].
5, the filter factor (or rectangular coefficient)
The filter factor is another representation of filter selectivity by measuring the filter selectivity using the ratio of the -60dB bandwidth of the filter's amplitude-frequency characteristic to the -3dB bandwidth. Ideal filter = 1, common filter = 1-5, obviously, the closer to 1, the better the filter selectivity.
Filter classification
Classification according to the frequency selection of the filter
Low pass filter
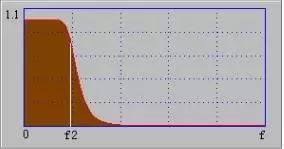
From 0 to f2, the amplitude-frequency characteristic is flat, which allows the frequency components below the f2 in the signal to pass almost without attenuation, while the frequency components above f2 are greatly attenuated.
High pass filter
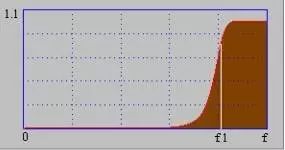
In contrast to low-pass filtering, the amplitude-frequency characteristics are flat from the frequency f1 to ∞. It allows the frequency components above the f1 in the signal to pass almost without attenuation, while the frequency components below f1 are greatly attenuated.
Bandpass filter
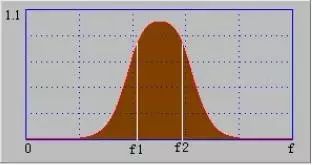
Its passband is between f1 and f2. It allows the frequency components in the signal above f1 and below f2 to pass without attenuation, while the other components are attenuated.
Band stop filter
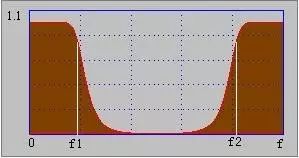
In contrast to bandpass filtering, the stopband is between frequencies f1 to f2. It attenuates the frequency components of the signal above f1 and below f2, and the signals of the remaining frequency components pass almost without attenuation.
The low-pass filter and the high-pass filter are the two most basic forms of the filter. Other filters can be decomposed into two types of filters. For example, the series connection of the low-pass filter and the high-pass filter is bandpass. The filter, the low-pass filter and the high-pass filter are connected in parallel as a band-stop filter.
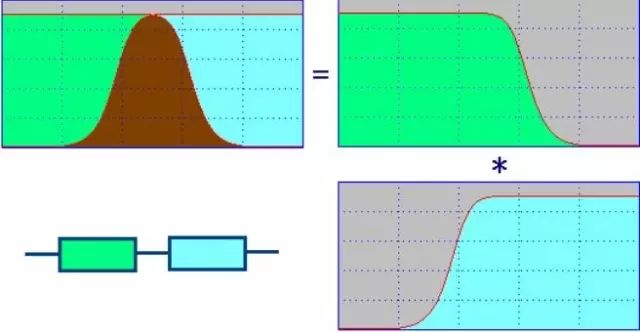
Series connection of low pass filter and high pass filter
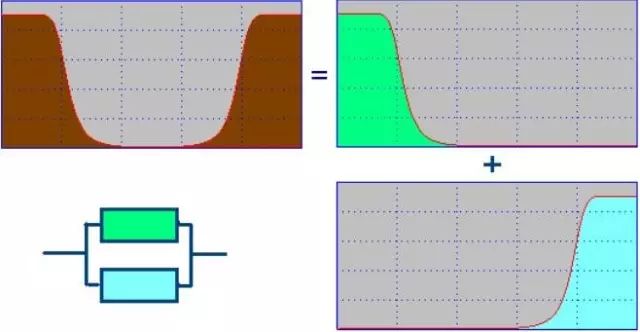
Parallel connection of low pass filter and high pass filter
Classified according to the "best approximation characteristics" standard
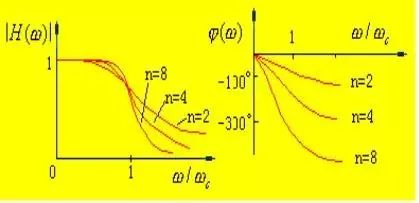
Butterworth filter
Requirements are imposed from the amplitude-frequency characteristics, regardless of the phase-frequency characteristics. The Butterworth filter has the largest flat amplitude characteristic, and its amplitude frequency response expression is:

Chebyshev filter
The Chebyshev filter also proposes approximation requirements in terms of amplitude-frequency characteristics. The amplitude-frequency response expression is:
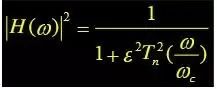
ε is the coefficient that determines the size of the passband ripple. The ripple is generated because the actual filter network contains reactive components; Tn is the first type of Chebyshev polynomial.
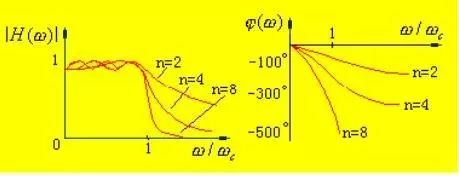
Compared with the Butterworth approximation, this characteristic has undulations in the passband, but the same value of n decays more steeply after entering the stopband, which is closer to the ideal. The smaller the ε value is, the smaller the passband undulation is, and the smaller the decibel value of the cutoff frequency point is, but the attenuation characteristic changes slowly after entering the stop band.
The Chebyshev filter is compared with the Butterworth filter. The Chebyshev filter has ripples in the pass and the transition strip is light and steep. Therefore, the Butterworth type is not allowed in the passband. More desirable; from the phase-frequency response point of view, the Butterworth type is better than the Chebyshev type, as can be seen from the comparison of the above two figures, the former's phase-frequency response is closer to a straight line.
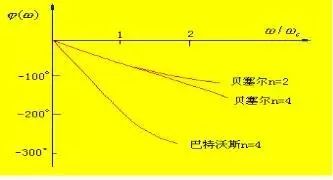
Bessel filter
Bessel filters are also known as flat-latency or constant-delay filters. Its phase shift is proportional to the frequency, which is a linear relationship. However, due to its poor amplitude-frequency characteristics, it often limits its application.
Divided into passive and active filters according to the components used
Passive filter
A passive filter consists only of passive components. It is constructed using the principle that the reactance of the capacitive and inductive components changes with frequency.
The advantages of this type of filter are: the circuit is relatively simple, does not require DC power supply, and has high reliability;
The disadvantage is that the signal in the passband has energy loss, the load effect is obvious, and the electromagnetic induction is easily caused when the inductance component is used. When the inductance L is large, the volume and weight of the filter are relatively large, and it is not applicable in the low frequency domain.
Active filter
The active filter consists of passive components and active components.
The advantage of this type of filter is that the signal in the passband not only has no energy loss, but also can be amplified, the load effect is not obvious, and the mutual influence is small when the multi-level associative, and the high-order filtering is easily formed by the simple method of cascading. And the filter is small in size, light in weight, and does not require magnetic shielding;
The disadvantage is that the passband range is limited by the bandwidth of the active device, and needs to be powered by a DC power supply. The reliability is not as high as that of the passive filter, and is not applicable in the case of high voltage, high frequency, and high power.
Divided into analog filter and digital filter according to the processed signal
Basic principle of digital filter
The signal processing procedure for importing a digital filter is shown in the figure. Analog signal (continuous signal)

Sampling must be performed using the sampling theorem. The input signal is subjected to analog low-pass filtering, an anti-aliasing filter, to remove high frequency components from the input signal. The smoothed analog signal is then used for sampling. In addition, after the DA conversion, the analog signal is smoothed by a smoothing filter, which can be done by an analog low-pass filter.
In addition, the digital equalizer used in digital communication can also be regarded as a digital filter, but when digital signal processing is directly performed by a digital equalizer, the AD converter and the DA converter in the figure are no longer needed. .
The so-called digital filter is to transform the input sequence into an output sequence through a certain operation. As shown in FIG. Its time domain input and output relationship is
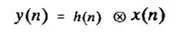
If the Fourier transform of x(n) and y (n) exists, the frequency domain relationship between the input and output is
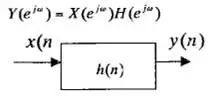
Assuming that |X(ejw)|, |H(ejw)| is as shown in (a) and (b) of the figure, |Y(ejw)| is obtained by the equation (c).
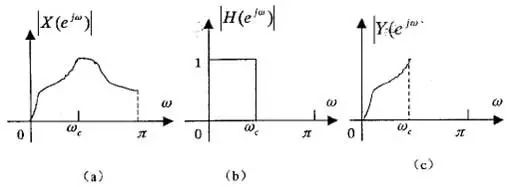
Thus, the result of x(n) passing through the system h(n) is such that the frequency portion of |w|>wc is no longer contained in the output y(n), and |w| The main features of the digital filter: 1. The digital filter is less sensitive to the external environment and has higher reliability. 2. The digital filter can realize functions such as accurate linear phase and multi-rate processing that cannot be realized by analog filters. 3. As long as the digital filter increases the word length, it can realize signal processing with arbitrary precision. 4. The digital filter is more flexible and can store signals at the same time. 5. The frequency domain width of the digitally processed signal is limited by the sampling rate. The main difference between digital filter and analog filter 1. Digital filters are used in discrete systems. Analog filters are used in continuous time systems and in discrete time systems such as SC (switched capacitor) filters. 2. A digital filter consists of an algorithm or device consisting of a digital multiplier, an adder, and a delay unit. The function of the digital filter is to perform arithmetic processing on the digital code of the input discrete signal to achieve the purpose of changing the spectrum of the signal. Digital filters can be implemented in computer software or in large-scale integrated digital hardware. Analog filters are active and passive, and active filters are primarily op amps, or spanning to op amps, and resistors and capacitors. Passive filters are mainly composed of R, L, and C. Analog filters have problems with voltage drift, temperature drift, and noise, and digital filters do not have these problems, resulting in high stability and accuracy. 3. From the perspective of the implementation means, the analog filter is generally built with capacitors and inductors. The digital filter can be realized by software or digital chip. It is very troublesome to replace the capacitor and the inductor when the analog filter parameters are changed. When the digital filter parameters are changed, sometimes it is only necessary to modify the coefficients (such as when the software is implemented). 4. From the technical indicators, it is very difficult to achieve an analog filter to achieve -60dB, and the digital filter can easily reach this index. 5. The biggest difference between analog and digital filters is that the digital filter is flipped about the Fs/2 frequency, which is symmetrical; the analog filter is not. Therefore, a large amount of interpolation filtering is selected in the DAC, and the image frequency is placed at a very distant frequency point, and then the analog frequency filter such as a sound meter is used to filter the image frequency in the RF section. So digital analog filters are indispensable. 6. The analog filter and the digital filter are expressed differently: the analog filter is represented by H(S), and the digital filter is represented by H(Z). The analog filter is dominated by the approximation of the amplitude-frequency characteristics, while the digital filter can achieve phase matching.
Phone Stand Holder Adjustable,Cell Phone Stand Holder,Phone Stand Holder Desk,Phone Stand Holder Hand,etc.
Shenzhen Chengrong Technology Co.ltd is a high-quality enterprise specializing in metal stamping and CNC production for 12 years. The company mainly aims at the R&D, production and sales of Notebook Laptop Stands and Mobile Phone Stands. From the mold design and processing to machining and product surface oxidation, spraying treatment etc ,integration can fully meet the various processing needs of customers. Have a complete and scientific quality management system, strength and product quality are recognized and trusted by the industry, to meet changing economic and social needs .

Phone Stand Holder Adjustable,Cell Phone Stand Holder,Phone Stand Holder Desk,Phone Stand Holder Hand
Shenzhen ChengRong Technology Co.,Ltd. , https://www.laptopstandsuppliers.com